| |
| • Про себе |
| • Новини |
| • Теор.Йм. |
| • Літ-ра (ТЙ) |
| • Тести |
| • Методички |
| • Таблиці |
| • Challenge |
| • Парадокси |
| • Спецкурси |
| • Sci. Lab. |
| • MathCad |
| • Ігротека |
| • Анекдот |
| • Газета |
|
Розклад каф. Розклад ф-ту Таймер Бібліотека ФКНК ОП + НП ФКНК |
|
Умова
Кошик містить \( N \) куль, позначених номерами від \( 1 \) до \( N \). Послідовно виймають \( n \) куль, повертаючи кулі назад. Нехай \( \xi \) – найбільший номер, який був вийнятий при цьому. Знайти ряд розподілу та функцію розподілу випадкової величини \( \xi \). Зобразити графік функції розподілу для випадку, коли \( N = 5 \) та \( n = 3 \).
Розв’язок
Формалізуємо простір елементарних подій $$\Omega = \{(a_1, a_2, \dots, a_n) \mid \forall i \in \{1,... , n\}, \ a_i \in \{1,... , N\} \},$$ тобто, з \( n \) витягнутих куль кожна мала деякий номер від \( 1 \) до \( N \). Тоді за теоремою добутку \(|\Omega| = N^n \).
Розглянемо подію $$A_k = \{\xi = k\} = \{(a_1, a_2, \dots, a_n) \in \Omega \mid \; \max a_i = k \},$$ тобто, серед \( n \) витягнутих куль (значення номерів кожної з яких може пробігати значення від \( 1 \) до \( N \)), максимальним серед номерів є номер \( k \). Відзначимо, що \(|A_k| = k^n - (k - 1)^n\), де зменшуване \( k^n \) є кількість векторів із \( n \) координатами, кожна координата яких може набувати значень від \( 1 \) до \( k \), а від’ємник \( (k - 1)^n \) є кількість векторів із \( n \) координатами, кожна координата яких може набувати значень від \( 1 \) до \( k - 1 \). Тоді за класичним визначенням ймовірності $$P(A_k) = \frac{k^n - (k - 1)^n}{N^n}.$$
Розглянемо ряд розподілу дискретної випадкової величини \( \xi \):
| \[ x_i \] | \[ 1 \] | \[ 2 \] | \[ \dots \] | \[ N-1 \] | \[ N \] |
| \[ p_i \] | \[ \frac{1^n - 0^n}{N^n} \] | \[ \frac{2^n - 1^n}{N^n} \] | \[ \dots \] | \[ \frac{(N-1)^n - (N-2)^n}{N^n} \] | \[ \frac{N^n - (N-1)^n}{N^n} \] |
Покажемо, що виконується характеристична властивість для цього ряду розподілу: $$\sum_{k=1}^{N} P(\xi = k) = \sum_{k=1}^{N} \frac{k^n - (k-1)^n}{N^n} = \frac{1}{N^n} \sum_{k=1}^{N} k^n - \sum_{k=1}^{N} (k-1)^n = \frac{1}{N^n} (N^n - 0^n) = 1.$$
Побудуємо функцію розподілу \(F_\xi(x) = P(\xi \leq x)\) дискретної випадкової величини \(\xi\):
- якщо \(x < 1\), то \(P(\xi \leq x) = 0\), бо \(\xi\) набуває лише значень із множини \(\{1,2\ldots,N\}\), тому для \(x < 1\) маємо, що \(F(x) = 0\);
- якщо \(k \leq x < k+1\), де \(k \in \overline{1,N-1}\), то \(P(\xi \leq x) = \sum\limits_{m=1}^k P(\xi = m) = \sum\limits_{m=1}^k \frac{m^n - (m-1)^n}{N^n} = \frac{k^n}{N^n}\), тому для \(k \leq x < k+1\) маємо, що \(F(x) = \left(\frac{k}{N}\right)^n\);
- якщо \(x \geq N\), то \(P(\xi \leq x) = 1\), бо всі значення, яких набуває дискретна випадкова величина \(\xi\), не перевищують \(N\), то для \(x \geq N\) маємо, що \(F(x) = 1\).
Отже, функція розподілу має наступний вид:
\[ F_\xi(x) = \begin{cases} 0 & x < 1, \\ \left( \frac{k}{N} \right)^n & k \leq x < k+1, \; k \in \overline{1, N-1}, \\ 1 & x \geq N. \end{cases} \]
Запишемо функцію розподілу для конкретного (\(N = 5\) та \(n = 3\)) випадку.
\[ F_\xi(x) = \begin{cases} 0 & x < 1, \\ \frac{1}{125} & 1 \leq x < 2, \\ \frac{8}{125} & 2 \leq x < 3, \\ \frac{27}{125} & 3 \leq x < 4, \\ \frac{64}{125} & 4 \leq x < 5, \\ 1 & x \geq 5 \end{cases} \]
Подамо схематичне зображення графіку цієї функції розподілу.
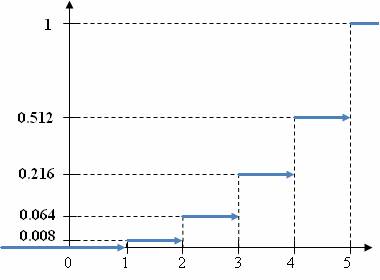
Відповідь: ряд розподілу наведений у розв’язку (див. табл.);
функція розподілу
\[
F_\xi(x) = \begin{cases}
0 & x < 1, \\
\left( \frac{k}{N} \right)^n & k \leq x < k+1, \; k \in \overline{1, N-1}, \\
1 & x \geq N.
\end{cases}
\]
графік функції розподілу для випадку, \(N = 5\) та \(n = 3\), наведено вище.


