| |
| • Про себе |
| • Новини |
| • Теор.Йм. |
| • Літ-ра (ТЙ) |
| • Тести |
| • Методички |
| • Таблиці |
| • Challenge |
| • Парадокси |
| • Спецкурси |
| • Sci. Lab. |
| • MathCad |
| • Ігротека |
| • Анекдот |
| • Газета |
|
Розклад каф. Розклад ф-ту Таймер Бібліотека ФКНК ОП + НП ФКНК |
|
СЛАБО?
Здесь будут сформулированы некоторые вопросы и задачи (как известные так пока и не решенные). Большинство задач и вопросов предназначены для студентов, но некоторые задачи будут интересны и профессионалам (знатокам ТВ, МС и т.д.), так что, если у Вас есть желание обсудить ту или иную задачу - пишите или приходите.
Итак, первой рассмотрим задачу про ханойские башни. Формулируется она очень просто - есть три стержня, на одном из которых N дисков разного диаметра. Надо переложить все диски на третий стержень, используя второй как вспомогательный, соблюдая два условия, во-первых, перекладывать можно только по одному диску, а во-вторых, никогда больший диск не должен быть над меньшим. Решение этой задачи известно, т.е. известен и алгоритм перекладывания дисков (как рекурсивный, так и нерекурсивный) и даже наименьшее необходимое число перекладываний. Вопрос: а сколько в среднем будет сделано перекладываний, если совершающий их человек не знает алгоритма и перекладывает диски исключительно наугад, соблюдая при этом два вышеуказанных правила? Попытайтесь решить эту задачу и получить ответ в явном виде для N=3 или N=4, а если сможете, то и для N=24.
Простая задача. В турнире каждая команда сыграла с каждой другой командой ровно по одному разу, причем 25% команд ни разу не выиграли. Сколько команд участвовало в турнире?
В самолёт, в котором 100 мест, собираются в порядке очереди зайти 100 пассажиров, первой из которых стоит старушка, которая садится на первое попавшееся место. Остальные пассажиры ведут себя нормально, т.е. занимают места согласно купленным билетам, и только если чьё-то место уже занято, то он занимает любое из свободных мест. Какая вероятность того, что последний стоящий в очереди займёт своё законное место? Как изменится решение, если рассмотреть другое число пассажиров (при условии, что количество мест всегда равно числу пассажиров)?
Какова вероятность того, что среди наудачу расставленных в ряд чисел от 1 до n ни одно число не займёт место со своим номером?
Сколько есть различных способов раскрасить 8 клеток в таблице 5х4 так, чтобы в каждой строке и в каждом столбце была хоть одна закрашенная клетка?
Задача Эйнштейна. Есть 5 домов, каждый разного цвета. В каждом доме живет по одному человеку отличной друг от друга национальности. Каждый пьет один и тот же напиток, курит определенную марку сигарет и держит определенное животное. (Цвет дома, национальность, напиток, марка сигарет и животное не повторяются).
Вопрос: кому принадлежит рыба?
Условия:
1) Англичанин живет в красном доме;
2) Швед держит собаку;
3) Датчанин пьет чай;
4) Зеленый дом стоит слева от белого;
5) Жилец зеленого дома пьет кофе;
6) Человек, который курит Pall Mall, держит птицу;
7) Жилец из среднего дома пьет молоко;
8) Жилец из желтого дома курит Dunhill;
9) Норвежец живет в первом доме;
10) Курильщик Marlboro живет около того, кто держит кошку;
11) Человек, который содержит лошадь, живет около того, кто курит Dunhill;
12) Курильщик сигарет Winfield пьет пиво;
13) Норвежец живет рядом с голубым домом;
14) Немец курит Rothmans;
15) Курильщик Marlboro живет по соседству с человеком, который пьет воду.
Эйнштейн придумал эту задачу в начале прошлого века и полагал, что лишь 2% жителей Земли смогут ее решить.
Решив эту задачу, попробуйте ответить на более сложные вопросы:
I. Какое одно из 15 условий можно убрать так, чтобы задача имела единственный тот же ответ?
II. Сколько разных ответов существует на предыдущий вопрос?
III. Какое максимальное число условий (и каких именно) можно убрать, чтобы задача имела единственный тот же ответ?
Попробуйте получить точный ответ в задаче про мосты для случая m = 4, n = 5.
Для 0 < t < 1 найти
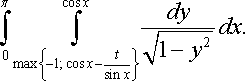
Здесь "найти" значит "представить в виде аналитический функции от t (без интеграла)". Это очень интересный и не очень простой интеграл. Впервые он "появился" при решении одной вероятностной задачи. У меня на него ушло несколько месяцев, а ответ оказался довольно красивым. И если приведенные выше задачи уже были решены ранее (решения можно найти в книгах или журналах, - за исключением дополнительных вопросов в задаче Эйнштейна), то этот интеграл пока что никто - кроме меня :) - взять не смог. Ни MathCad, ни Mathematica, ни Wolfram Alpha не справились. Если бы найти спонсора, можно было бы назначить денежный приз тому, кто первым пришлет решение этой задачи :)
Вот еще одна коварная задача, уходящая корнями в теорию вероятностей, но которую можно очень компактно и красиво сформулировать
в терминах алгебры. Итак, предположим, что у нас есть квадратная бинарная матрица (т.е. все ее элементы это 0 и 1)
У этой задачи есть очень красивое не-алгебраическое решение (так сказать, на пальцах его можно донести и до школьника). Интересно, а есть ли красивое алгебраическое решение?


