| |
| • Про себе |
| • Новини |
| • Теор.Йм. |
| • Літ-ра (ТЙ) |
| • Тести |
| • Методички |
| • Таблиці |
| • Challenge |
| • Парадокси |
| • Спецкурси |
| • Sci. Lab. |
| • MathCad |
| • Ігротека |
| • Анекдот |
| • Газета |
|
Розклад каф. Розклад ф-ту Таймер Бібліотека ФКНК ОП + НП ФКНК |
|
Умова
В лотереї випустили 100 білетів, серед яких один білет виграє 10000 гривень і 10 білетів виграють по 1000 гривень. Знайти ряд розподілу та функцію розподілу для випадкової величини \(X\) – можливий виграш для власника одного лотерейного білета.
Розв’язок
З умови задачі випливає, що випадкова величина \(X\) може приймати наступні значення: 0, 1000 та 10000 (тобто, гравець може нічого не виграти, виграти 1000 гривень чи зірвати джекпот у розмірі 10000). Також легко визначити ймовірності, з якими \(X\) набуває цих значень, а саме:
\[ P(X = 0) = \frac{89}{100} = 0.89, \] \[ P(X = 1000) = \frac{10}{100} = 0.1, \] \[ P(X = 10000) = \frac{1}{100} = 0.01. \]
Отже, ряд розподілу набуває виду:
| \[ X_i \] | 0 | 1000 | 10000 |
| \[ p_i \] | 0.89 | 0.1 | 0.01 |
Відзначимо, що виконується характеристична властивість ряду розподілу: \[ \sum_{i=1}^{3} p_i = 0.89 + 0.1 + 0.01 = 1. \]
Далі будуємо функцію розподілу \( F(x) = F_X (x) = P(X \leq x) \) випадкової величини \( X \):
- якщо \( x < 0 \), то очевидно, що \( P(X \leq x) = 0 \), бо випадкова величина \( X \) набуває лише невід’ємних значень (див. таблицю), тому для \( x < 0 \) маємо \( F(x) = 0 \);
- якщо \( 0 \leq x < 1000 \), то \( P(X \leq x) = P(X = 0) = 0.89 \), тому для \( 0 \leq x < 1000 \) маємо \( F(x) = 0.89 \);
- якщо \( 1000 \leq x < 10000 \), то \( P(X \leq x) = P(X = 0) + P(X = 1000) = 0.89 + 0.1 = 0.99 \), тому для \( 1000 \leq x < 10000 \) маємо \( F(x) = 0.99 \);
- якщо \( x \geq 10000 \), то \( P(X \leq x) = 1 \), бо всі значення, яких може набувати випадкова величина \( X \), не перевищують 10000 (див. таблицю), тому для \( x \geq 10000 \) маємо \( F(x) = 1 \).
Отже, функція розподілу набуває такого виду: \[ F(x) = \begin{cases} 0, & x < 0, \\ 0.89, & 0 \leq x < 1000, \\ 0.99, & 1000 \leq x < 10000, \\ 1, & x \geq 10000. \end{cases} \]
Графік функції розподілу:
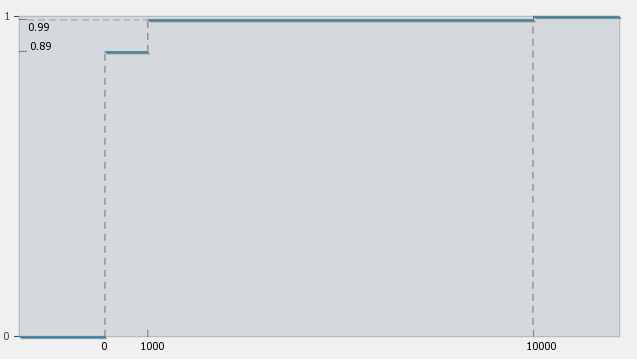
Для того, щоб було легше сприймати графік, наведемо його схематичне зображення (коли масштаб не зберігається):
Відповідь:
ряд розподілу:
| \[ X_i \] | 0 | 1000 | 10000 |
| \[ p_i \] | 0.89 | 0.1 | 0.01 |


