Двовимірні
випадкові вектори
Задача 12.1 Двовимірна дискретна випадкова величина (ξ,η) задана таблицею розподілу
|
|
3 |
8 |
10 |
|
-1 |
0,17 |
0,13 |
0,25 |
|
0 |
0,1 |
0,3 |
0,05 |
а) Знайти умовний
розподіл ξ при η = –1.
б) Чи залежні ξ
та η ?
Задача 12.2 Двовимірний випадковий вектор (ξ,η) має розподіл
|
|
0 |
1 |
|
-1 |
0,1 |
0,2 |
|
0 |
0,2 |
0,3 |
|
1 |
0 |
0,2 |
Знайти Мζ, Dζ , де ζ = 2ξ + η2.
Задача 12.3 Випадкова точка на площині (ξ,η) має розподіл
|
|
0 |
1 |
|
-1 |
0,1 |
0,15 |
|
0 |
0,15 |
0,25 |
|
1 |
0,2 |
0,15 |
Знайти Мξ, Мη, Dξ, Dη, cov(ξ,η) та ρξ,η.
Задача 12.4 Випадковий вектор (ξ,η) має Мξ=0, Мη=2, Dξ=2, Dη=1 та коефіцієнт кореляції . ζ=2ξ–3η. Знайти Мζ та Dζ.
Задача 12.5 В продукції заводу браку через дефект А
складає 3%, а через дефект В – 4,5%. Небракованої продукції 95%. Знайти
коефіцієнт кореляції дефектів А та В.
Домашнє завдання №12.
1. Із коробки, в якій 3
червоних та 3 зелених олівці, послідовно без повернення витягають олівці до
появи першого червоного олівця. Нехай ξ – кількість витягнутих при цьому
олівців. Потім продовжують витягати олівці до появи першого зеленого олівця.
Нехай η – кількість витягнутих при цьому олівців (в другій серії). Скласти
закон розподілу вектора (ξ,η), знайти його числові характеристики. Чи залежні ξ
та η?
Додаткові задачі
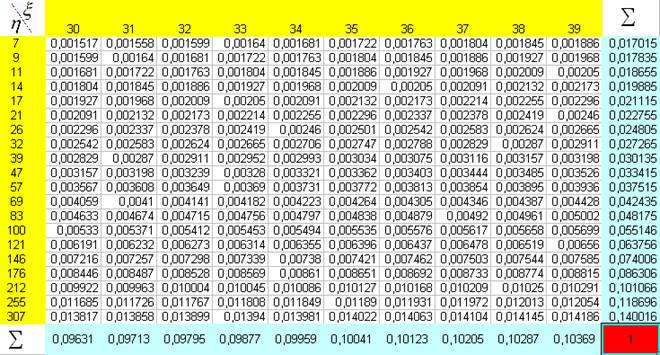
1. Використовуючи Excel, знайти всі параметри розподілу випадкового
вектора, розподіл якого задано наступною таблицею (pzas_seminar_12.xls):