Заняття №6
Математичне сподівання та дисперсія дискретної в.в.
Задача 6.1 Нехай Х – дискретна випадкова величина з розподілом
|
Хі |
-1 |
0 |
1 |
|
рі |
0.2 |
0.3 |
? |
Знайти математичне сподівання та дисперсію випадкової величини Х4.
Задача 6.2 В лотереї розігрують мотоцикл за 250 умовних грошових одиниць (у.о.), велосипед – за 50 у.о. і годинник за 40 у.о. Знайти математичне сподівання виграшу для людини, у якої 1 білет, якщо всього 100 білетів.
Задача 6.3 Із ящика, в якому 2 білих та 4 чорних кулі, виймають 3 кулі і перекладають в інший ящик, де вже було 5 білих куль. Потім з другого ящика перекладають 4 кулі знову до першого ящика. Знайти математичне сподівання числа білих куль х1 та х2 в обох ящиках.
Задача 6.4 При киданні трьох гральних кубиків гравець виграє 18 гривень, якщо випадають три шістки, 1,4 гривні – якщо випаде лише дві шістки, 0,2 гривні – якщо випаде одна шістка. Якою має бути ставка за участь у грі, щоб гра була нешкідливою (рос. – безобидной)?
Задача 6.5 Х1 – число очок на одному гральному кубику, Х2 – сума очок при киданні двох гральних кубиків. Знайти математичні сподівання та дисперсії випадкових величин Х1 та Х2.
Задача 6.6 Монету підкидають до першої появи герба. Знайти середнє число підкидань.
Домашнє завдання № 6.
- По мішені, ймовірність влучити в яку є р, стріляють, доки не набереться k влучень. Знайти функцію розподілу та математичне сподівання числа пострілів.
- Із ящика, в якому m білих та n чорних куль, дістають і повертають назад кулі до тих пір, доки не витягнуть білу кулю. Знайти математичне сподівання числа X витягнутих чорних куль.
3 Із ящика, в якому w1 білих та b1 чорних куль, виймають n1 куль і перекладають в інший ящик, де вже було w2 білих куль та b2 чорних куль. Потім з другого ящика перекладають n2 куль знову до першого ящика. Знайти математичне сподівання числа білих куль х1 та х2 в обох ящиках.
Варіанти:
|
Варіант № |
w1 |
b1 |
n1 |
w2 |
b2 |
n2 |
|
1 |
2 |
4 |
3 |
5 |
2 |
4 |
|
2 |
3 |
4 |
3 |
5 |
2 |
4 |
|
3 |
2 |
5 |
3 |
5 |
2 |
4 |
|
4 |
2 |
4 |
4 |
5 |
2 |
4 |
|
5 |
2 |
4 |
3 |
6 |
2 |
4 |
|
6 |
2 |
4 |
3 |
5 |
3 |
4 |
|
7 |
1 |
4 |
3 |
5 |
2 |
4 |
|
8 |
2 |
3 |
3 |
5 |
2 |
4 |
|
9 |
2 |
4 |
2 |
5 |
2 |
4 |
|
10 |
2 |
4 |
3 |
4 |
2 |
4 |
|
11 |
2 |
4 |
3 |
5 |
4 |
4 |
|
12 |
2 |
4 |
3 |
5 |
2 |
3 |
Відповідь дати з точністю до 10-3.
Додаткові задачі
1. Навмання обирається число x із чисел {1, 2, … , N}, а потім із множини {x, x+1, … , N} навмання обирається число h. Знайти розподіл випадкової величини h (в загальному випадку та при N=5).
2. “Тріель”: троє приймають участь в “трикутній” дуелі на пістолетах. Всім добре відомо, що А влучає з ймовірністю 0.3, В – з ймовірністю 1, а С – з ймовірністю 0.5. Вони стріляють по черзі (перший – А ...), поранений чи вбитий вибуває, і все це триває до тих пір, доки один з них не залишиться. Яку стратегію має обрати гравець А, щоб найімовірніше виграти?
3. Дискретна випадкова величина x задана рядом розподілу ймовірностей:
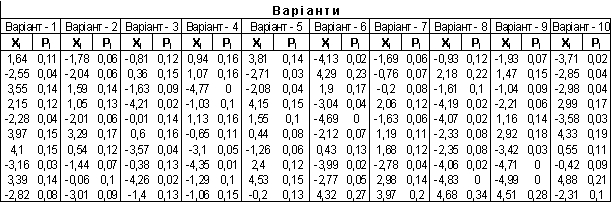
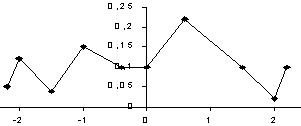
Для x побудувати :
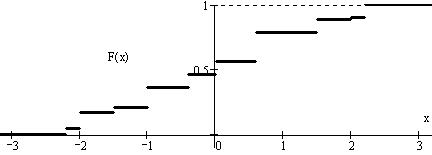
1) функцію розподілу (графік),
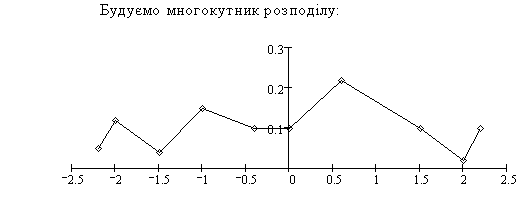
2) многокутник розподілу;
Порахувати :
3) математичне сподівання та дисперсію,
4) всі моменти (до четвертого включно) - початкові та центральні,
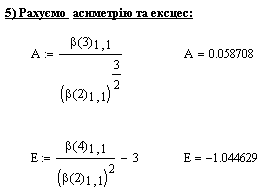
5) асиметрію та ексцес.
Приклад розв’язування (MathCad2001Pro)
![]()

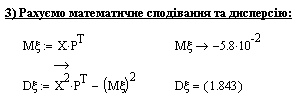
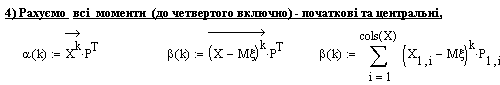
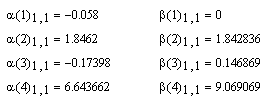
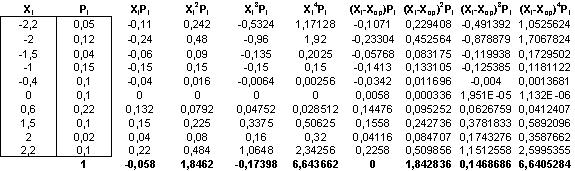
Приклад розв’язування (XL)
![]()