Заняття №4
Геометричні ймовірності
Задача 4.1 Двоє людей А та В домовилися зустрітися між 18 та 19 годинами. Кожен з них, прийшовши в довільний (рівно можливий) момент часу між 18 та 19 годинами, чекає 15 хвилин і йде. Яка ймовірність того, що А та В зустрінуться?
Задача 4.1.1 Двоє людей домовились зустрітись між першою та другою годинами на таких умовах: той, хто прийде першим чекає на другого не більше ніж 20 хвилин. Знайти імовірність їх зустрічі – події А.
Задача 4.2 На площині проведено паралельні прямі на відстані 8 см одна від одної. Знайти ймовірність того, що навмання кинутий на цю площину круг радіуса 3 см не перетне жодну з ліній.
Задача 4.3 На відрізку довжини L навмання беруться 2 точки, в результаті чого відрізок ділиться на 3 нові відрізки. Знайти ймовірність того, що з цих трьох нових відрізків можна скласти трикутник.
Задача 4.4 Маємо 6 відрізків, довжини яких 2, 4, 6, 8, 10 та 12 см. Знайти ймовірність того, що з трьох навмання вибраних відрізків (з цих шести) можна буде скласти трикутник.
Задача 4.5 Маємо рівняння x2 + ax + b = 0 , де a та b довільно (рівно можливо) обираються з відрізка [ 0 , 1 ]. Знайти ймовірність того, що це рівняння має дійсні корені.
Задача 4.6 На відрізок ½АВ½=12 см навмання кидають точку М. Знайти ймовірність того, що площа квадрата зі стороною АМ буде від 36 до 81 см2.
Задача 4.7 Знайти ймовірність того, що сума двох додатних правильних дробів не більша від 1, а їх добуток не більший від .
Домашнє завдання № 4.
- Знайти ймовірність того, що корені квадратного рівняння x2 + 2bx + c = 0 дійсні. Застосувати той же метод, що і в задачі 4.5, тільки квадрат взяти з центром в точці (0,0), а потім спрямувати його розмір у нескінченність. Чи зміниться відповідь, якщо замість квадрата брати інші фігури? Спробувати взяти а) чотирикутник (теж з центром у початку координат) ширини 2k і висоти 2k2, б) круг (теж з центром у початку координат), в) ромб з діагоналями 4а (вздовж вісі ОY) та 2а (вздовж вісі ОX) (теж з центром у початку координат).
- На безмежну шахову дошку зі стороною квадрата а кидають монету радіуса . Знайти ймовірності таких подій: А={монета потрапить в середину квадрата}, B={Монета перетне не більше ніж одну сторону квадрата}.
- На колі навмання взято три точки А, В та С. Знайти ймовірність того, що трикутник АВС а) прямокутний; б) правильний; в) гострокутний.
Д о д а т к о в і з а д а ч і
Задача №1
Точка обирається з відрізка і ділить його на більшу (h1) та меншу (h2) частини. Знайти P{h1 £ x} та P{h2 £ x}, де xÎR.
Задача №2
Точка А має рівномірний розподіл в квадраті зі стороною a. Знайти ймовірність того, що відстань від точки А до найближчої сторони квадрата буде менше, ніж відстань від точки А до найближчої діагоналі квадрата.
Задача №3
(Задача Бюффона для l<a)
Площину розграфлено паралельними прямими, відстань між якими 2а. На площину кидають голку довжини 2l<2a. Яка ймовірність того, що голка перетне одну з прямих?
Задача №4
(Задача Бюффона для l>a)
Площину розграфлено паралельними прямими, відстань між якими 2а. На площину кидають голку довжини 2l>2a. Яка ймовірність того, що голка перетне одну з прямих?
Задача №5
Яка ймовірність того, що напівсфера, кинута на площину, впаде на неї своєю плоскою частиною?
Задача №6
В інтервалі [0, T] у випадковий момент u з’являється сигнал, довжини D. Приймач вмикається у випадковий момент vÎ[0, T] на час t. Яка ймовірність того, що сигнал буде прийнято? (Розв’язати задачу в загальному випадку і при T=4, D=3, t=2)
Задача №7
Автобус ходить кожні T1 хвилин, тролейбус – кожні T2 хвилин. Пасажир чекає чи автобус чи тролейбус. Яка ймовірність, що він буде чекати не довше ніж t хвилин (0< t <min{T1,T2})? (Розв’язати задачу в загальному випадку і при T1=4, T2=3, t=2)
Задача №8
Точку з координатами (x,h) навмання кидають в квадрат зі стороною 1. Довести, що для довільних x,yÎR події A={x<x} та В={h<y} незалежні.
Задача №9
Точку з координатами (x,h) навмання кидають в трикутник з вершинами (1,0), (0,0) та (0,1). Довести, що події A={x<1/2} та В={h<1/2} залежні.
Задача №10
В круг з діаметром АВ=2а навмання кидають точку С. Яка ймовірність того, що ця точка виявиться ближче до діаметра АВ, ніж до кола?
Задачі підвищеної складності
1. На площину, розграфлену паралельними прямими, відстань між якими дорівнює 3, навмання кидають голку довжиною 5. Знайти ймовірність того, що голка перетне принаймні одну з паралельних прямих.
2. На площину, розграфлену паралельними прямими, відстань між якими дорівнює 3, навмання кидають голку довжиною 7. Знайти математичне сподівання числа перетинів прямих голкою.
3. На площину кидають навмання квадрат, сторона якого дорівнює 10. Знайти математичне сподівання числа точок перетину сторін квадрата з паралельними прямими, відстань між якими дорівнює 10.
4. На площину кидають навмання квадрат, сторона якого дорівнює 10. Знайти розподіл числа точок перетину сторін квадрата з паралельними прямими, відстань між якими дорівнює 10. (Відповідь має узгоджуватись з відповіддю з попередньої задачі).
Парадокс Бертрана
(Josef Bertrand, “Calcul des Probabilities”, 1888)
Для кола навмання обираємо довільну хорду. Яка ймовірність того, що ця хорда довша від сторони правильного трикутника вписаного в це коло?
|
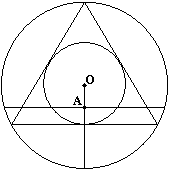
1-ий розв¢язок: В колі вибираємо довільну точку А і будуємо хорду так, щоб А була її серединою. Хорда буде довшою за сторону вписаного трикутника, якщо ця точка А лежатиме в колі, вписаному в цей трикутник, тому
|
|
|
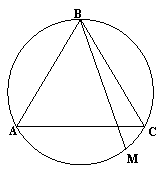
2-ий розв¢язок: Можна вважати, що один кінець хорди співпадає з вершиною трикутника, тоді
|
|
|
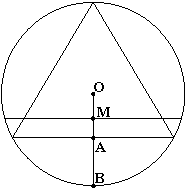
3-ій розв¢язок: Виберемо точку М на радіусі кола і виберемо хорду, яка перпендикулярна цьому радіусу і проходить через дану точку М. Тоді ця хорда буде більша за сторону вписаного трикутника, якщо точка М лежить на ОА ( |OA| = r), а не на АВ (|OB|=R=2r), тому
|
|
Дивно, що всі три розв’язки дають різні відповіді. Парадокс...