Заняття 3
(другий семестр)
Марківські ланцюги
із скінченою множиною станів
та дискретним часом
Задача 3.1 Довести, що P(n) = Pn.
Задача 3.2 ξ0,
ξ1, ξ2,
... послідовність
незалежних однаково розподілених ( P{ξi = ±1} =
) випадкових величин. Розглядається нова послідовність випадкових величин ηn =
(ξn + ξn+1). Знайти pjk(m, n) = P{ ηn = k | ηm = j }. Довести, що {ηn | n ≥ 1} не є ланцюгом Маркова.
Задача 3.3 P стохастична матриця (сума елементів кожного
рядка = 1 і всі елементи невід’ємні). Довести що
n>1 P(n)
теж стохастична матриця.
Задача 3.4 H={1, 2, … m}, i → j . Довести, що n≤m:
>0.
Задача 3.5 По виду матриці ймовірностей переходів за один крок зробити класифікацію станів відповідного марківського ланцюга:
а) б)
в)
Задача 3.6 Довести, що матриця В перехідних ймовірностей, які відповідають переходам всередині деякого суттєвого класу, теж стохастична.
Задача 3.7 Виразити через відповідні ймовірності переходів за k кроків та через початковий розподіл наступні умовні ймовірності
а) P{ξ0 = i | ξn = j }, б) P{ξr = k | ξ0 = i, ξn = j}, якщо 0 < r < n .
Задача 3.8 Побудувати приклад зліченого марківського ланцюга, у якого всі стани несуттєві. Чи можна це зробити для скінченого марківського ланцюга?
Домашнє завдання 3.
1. По виду матриці ймовірностей переходів за один крок зробити класифікацію станів відповідного марківського ланцюга:
г) д)
е)
2. Розглядатимемо ланцюг Маркова, пов’язаний зі схемою випробувань Бернуллі з двома результатами У − успіх і Н − невдача (імовірність результату У дорівнює р), так: вважатимемо, що ланцюг Маркова Хn знаходиться в стані 1, якщо (n-1)-е і n-те випробування привели до результатів УУ. Аналогічно стани 2, 3, 4 відповідають парам результатів УН, НУ, НН. Знайти матрицю P перехідних імовірностей ланцюга Маркова Хn та стаціонарний розподіл (це такий початковий розподіл ймовірностей по станах ланцюга, який не змінюється від кроку до кроку). Чи буде природній початковий розподіл (тобто той, що логічно випливає зі схеми незалежних випробувань Бернуллі) стаціонарним?
3. Говорять, що стан j досягається зі тану i (позначається i→j), коли існує таке n, що . Довести, що із співвідношень i → j та j → k випливає, що й i → k.
Додаткові задачі з розібраним прикладом.
(Класифікація станів марківського ланцюга)
Нехай матриця ймовірностей переходів за один крок однорідного марківського ланцюга наступна:

0. Малюємо граф:

1. Перевіримо, чи є ця матриця стохастичною.
Оскільки всі елементи цієї матриці невід’ємні, а сума елементів кожного рядка дорівнює одиниці, то ця матриця справді є стохастичною.
2. Визначимо, чи є даний ланцюг періодичним.
Аналізуючи матрицю Р (чи відповідний граф), доходимо висновку, що у перший, третій та п’ятий стани можна повернутися за кількість кроків від 2 до 7, у другий та сьомий стани − лише за парну кількість кроків (2, 4 та 6), у четвертий стан − лише за 2, 4, 5, 6 та 7, у шостий − від 2 до 7 кроків. Найбільшим спільним дільником знайдених кроків повернення є 1, а це означає, що цей ланцюг не має періоду.
3. Визначимо, чи є даний ланцюг незвідним.
Аналізуючи матрицю Р (чи відповідний граф), доходимо висновку, що даний ланцюг є звідним, бо розбивається на класи досяжності.
4. Для звідного ланцюга виділимо суттєві (істотні) класи та клас неістотніих (несуттєвих) станів.
Аналізуючи матрицю Р (чи відповідний граф), доходимо висновку, що стани 2 та 7 утворюють суттєвий клас (з очевидним періодом = 2), бо з 2 можна потрапити в 7 і навпаки, а вийти з цього класу неможливо. Всі інші стани − несуттєві, бо з кожного з них можна потрапити в сьомий стан і вже не повернутися.
Отже: {2, 7} − суттєвий клас з періодом = 2, {1, 3, 4, 5, 6} − клас несуттєвих станів.
Висновки: ланцюг не має періоду, є звідним, {2, 7} − суттєвий клас з періодом = 2, {1, 3, 4, 5, 6} − клас несуттєвих станів.
Власне додаткові задачі: Зробити класифікацію станів однорідного марківського ланцюга, який має наступну матрицю ймовірностей переходів за один крок:
1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  7)
7) 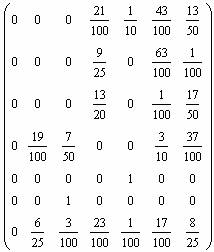 8)
8)  9)
9) 
Задачі підвищеної складності.
1. Нехай ξ0, ξ1 … - незалежні однаково розподілені випадкові
величини, що набувають значень 1
та 1 відповідно з імовірностями 1-р та р, і нехай ηn = ξn·ξn+1. Чи буде послідовність ηn ланцюгом Маркова? Чи існує границя ймовірностей P{ηn = −1} при n → ∞ ?
2. Довести, що для марківського ланцюга з дискретним часом та зліченою множиною станів мають місце наступні варіанти марківської рівності:
|
P{ξn+1 = Xn+1
| ξn = Xn, ξn−1 = P{ξn+1 = Xn+1 | ξn = Xn } |
(1) |
|
P{ξn+1 = P{ξn+1 |
(2) |